참고강의
https://www.youtube.com/watch?v=jaPPALsUZo8
강의노트
원본 -> 노이즈 로 갔다가 다시 노이즈 -> 원본으로 돌아오면서, 디노이징하는 법을 학습하는 것. (앱실론학습)
디노이징 하는 법을 다 익힌 모델은 노이즈에서 정규분포에 따른 latent value로 새로운 이미지를 생성할 수 있음.




Forward process
: 이미지-> 가우시안노이즈 (정규분포, N(m,시그마제곱)= N(0,1))로 만드는 과정
X0 ----------> Xt-1 ------> Xt

Xt = a * Xt-1 + b*noise
Xt는 그전시점의 Xt-1에 (weight는 아니고 상수) 곱한것 + bias에 노이즈곱한것이다.
상수값 a와, bias b를 베타로 다시 표현함.
루트1-베타t의 제곱 * 베타t의 제곱 = 1 이 되게 해서, N(0,1)로 만들기 위한 의도로 수식일 바꾼것.

Reverse process
: 가우시안 노이즈 -> 이미지

VAE는 x1 -> z1 encoding - > decoded X1' 이렇게 단 한번의 과정이라면,
diffusion은 잠재벡터 z가 여러번 반복되는 VAE의 모습임
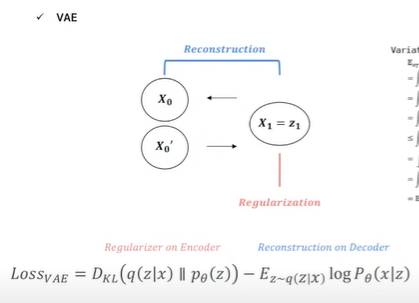
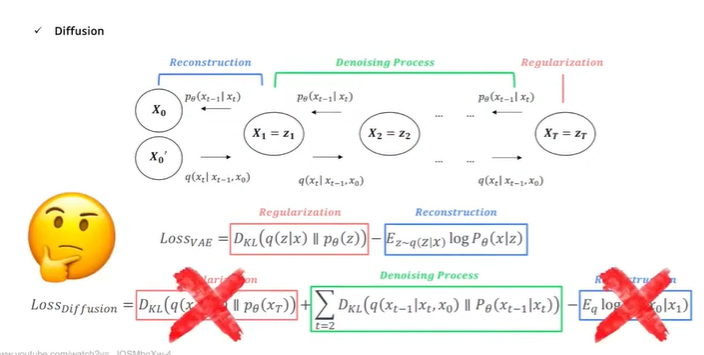

DDPM (Denoising Diffusion Probabilistic Models, 2020)
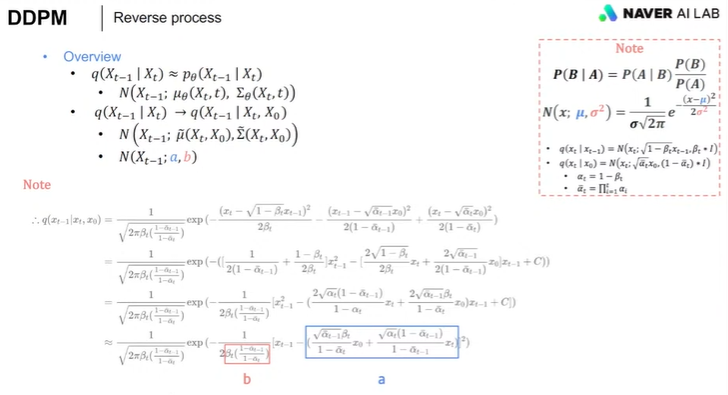


DDIM (Denoising Diffusion Implicit Models, 2021)
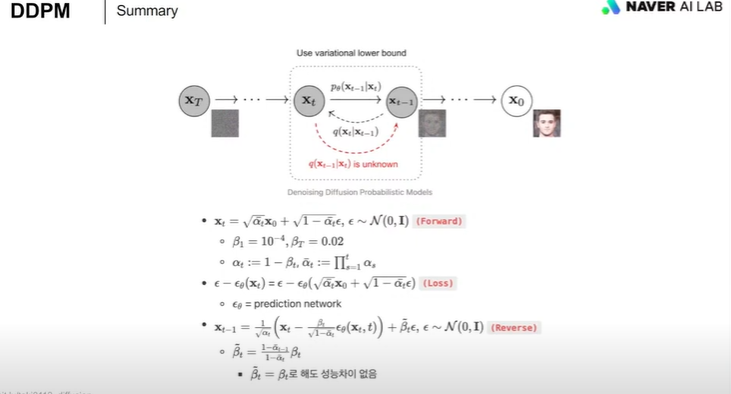
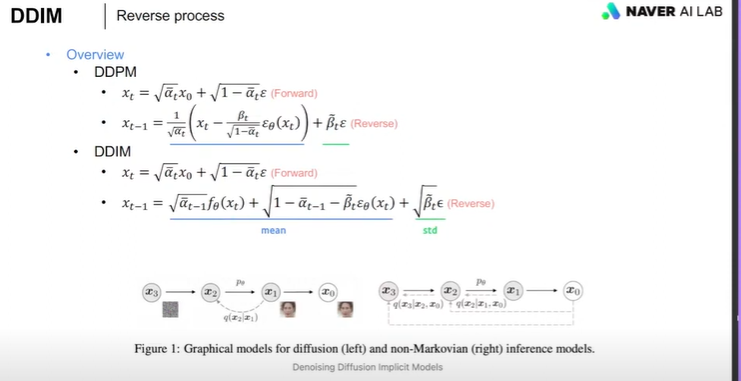
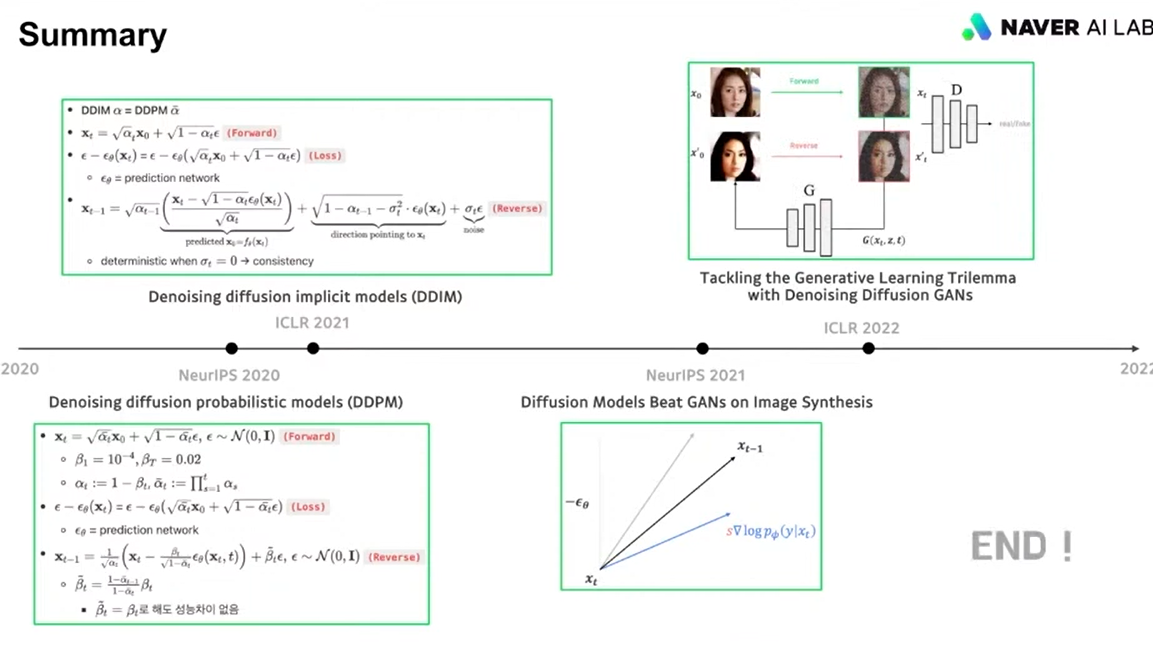
다시 DDPM을 정리하면,
포워드프로세스의 Xt는 X0로부터 어떤노이즈를 더해주는데 저런식으로 알파 햇으로 표현을 했구나.
리버스의 xt-1는 노이즈낀 xt로부터 리버스 거친거구나, 괄호 안은 평균값이구나.
근데 이건 다 markov의 정의가 기반이 되어서, Xt는 Xt-1로 인한다는 시계열의 성질을 가지는데,,
즉, 리버스 할 때, t가 1000번이라면, X0부터 X1000까지 추론(인퍼런스)과정을 천번 거쳐서 와야하는데,
이거를 깨고, non-markov라고 가정하고 그냥 X0 - X1000까지의 값을 받아서 바로 계산하는 것이 DDIM.
밑에보면 인퍼런스, 즉 리버스 개념만 다른거라서 포워드는 식이 같고, 리버스만 달라짐.
하지만 이마저도 평균과 분산의 꼴은 동일.
DDPM은 X77에서 t0(원본이미지)를 예측하려면 77,76,75,...,0까지 77번 인퍼런스 해야하지만
DDIM은 X77 이 아니라 어떤 것도 바로 혹은 몇번 스텝으로 점핑하며 77번보다 간소화해서 X0를 예측할 수 있음.

Diffusion Models Beat GANs on Image Systhesis (2021) - a.k.a Guided Diffusion
디퓨젼이 gan을 이기기 시작.
DDPM, DDIM은 그냥 유넷구조라서 이 구조를 좀 더 발전시킨 것.
(멀티헤드어텐션, 멀티레졸루션어텐션, AdaGN)
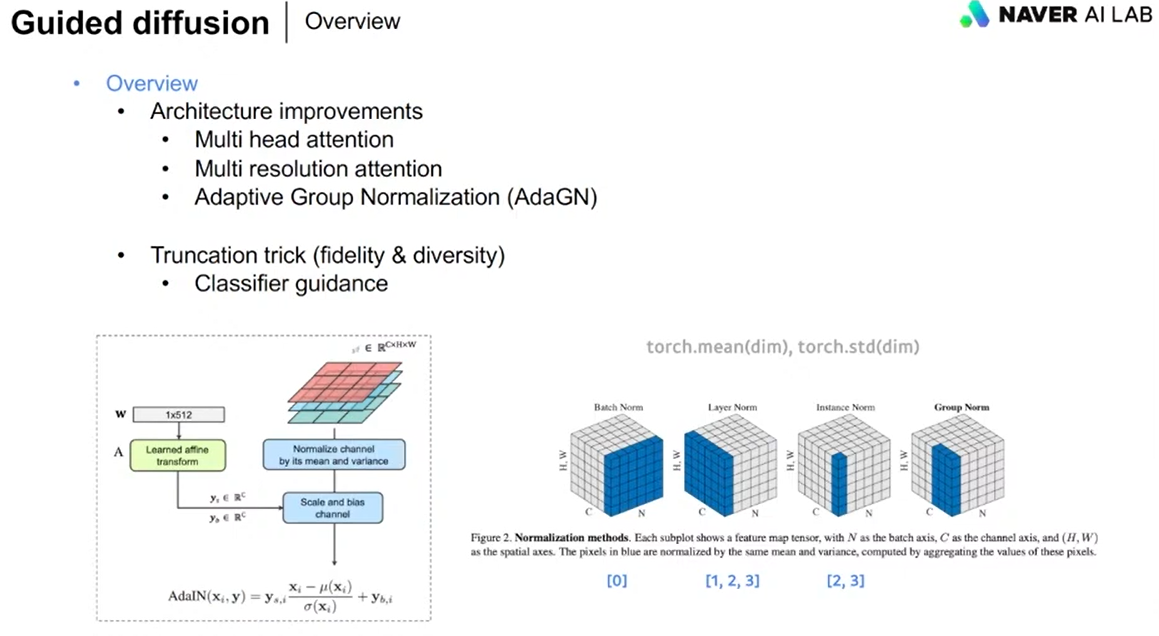
Truncation trick : fidelity(이미지퀄리티)과 diversity(다양성)은 trade-off 관계라서 이 끝단을 얼마나 자르느냐 하는 것
좌변 : 노이즈낀 xt+1과 라벨(개,고양이)y가 주어졌을 때, 디노이징된 xt의 분포(p세타)는 우변과 같이 표현될 수 있다.
우변 : 노이즈낀 xt이미지로부터 레이블을 구한분포와(우측) 노이즈낀 xt+1과 디노이즈된 xt 분포(좌측)의 곱이다.
Z는 그냥 상수.
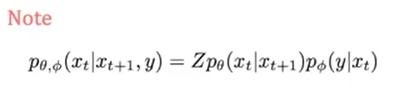
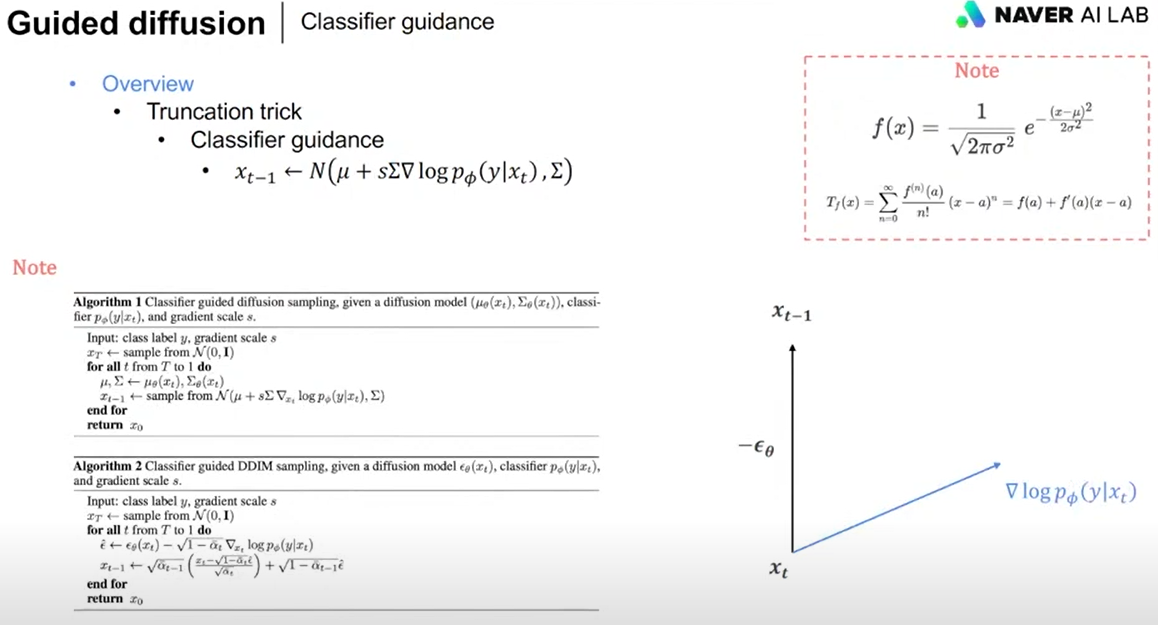
xt라는 노이징 이미지가 주어졌을 때, xt-1방향으로 앱실론(노이즈)를 빼는 방향으로 진행이 될텐데
여기에 s (클래스 레이블로 갈 수 있게 하는 어떤 변화량 gradient)가 벡터로 다른 방향을 더하게 되면,
벡터는 당연 방향이 달라진다.
s가 강하게 반영된다는 뜻은, s의 레이블이 될 수 있도록 이미지를 만들라는 거라서 fidelity는 올라가지만 다양성은 줄어듬
s가 약하게 반영된다는 뜻은, s의 레이블이 되는 방향으로 힘을 많이 주지 않는다는거니 diversity는 올라가고 성능은 떨어짐.
Tackling the Generative Learning Trilemma with Denoising Diffusion GANs (NVIDIA, 2022)
디퓨젼이랑 GAN이랑 합친것
포워드는 고대로 하고, 리버스도 고대로 하는데,,
DDIM은 x'0를 수학적으로 예측하고, 단계를 거쳐 노이즈를 재공했었는데, GAN은 단계없이 바로 x'0를 예측하게 하니까 훨씬 빠름.
xt는 완전한 가우시안 노이즈이니,,
1. diffusion forward로 x0이미지에 노이즈 추가하고, 리버스 할 때 노이즈낀 xt-1를 만듬 (diffusion forward)
2. xt-1를 GAN의 generator에게 넣어 x'0(원본비슷)을 생성하게 함. (GAN)
3. diffusion forward로 GAN이 생성한 x'0과 diffusion forward가 만든 노이즈낀 xt를 인풋으로 받아서
리버스 과정을 거쳐 xt에서 x't-1을 만들어 냄 (diffusion reverse)
4. GAN의 discriminator가 xt-1(실제이미지x0+노이즈)와 x't-1(생성이미지x'0+노이즈)의 두 이미지를 노이즈를 빼면서 비교하여 real/fake를 감별함 (GAN)
diffusion 모델에서 앱실론을 학습시켰던 이유는 x'0을 다시 예측해내야 하기 때문이었는데,
DDGAN 같은 경우는 x'0이 GAN네트워크로 나오기 때문에
사실 forward, reverser diffusion을 할 때 디퓨젼 네트워크가 쓰이는 것은 아니고, 수식만 가져다 쓴다.
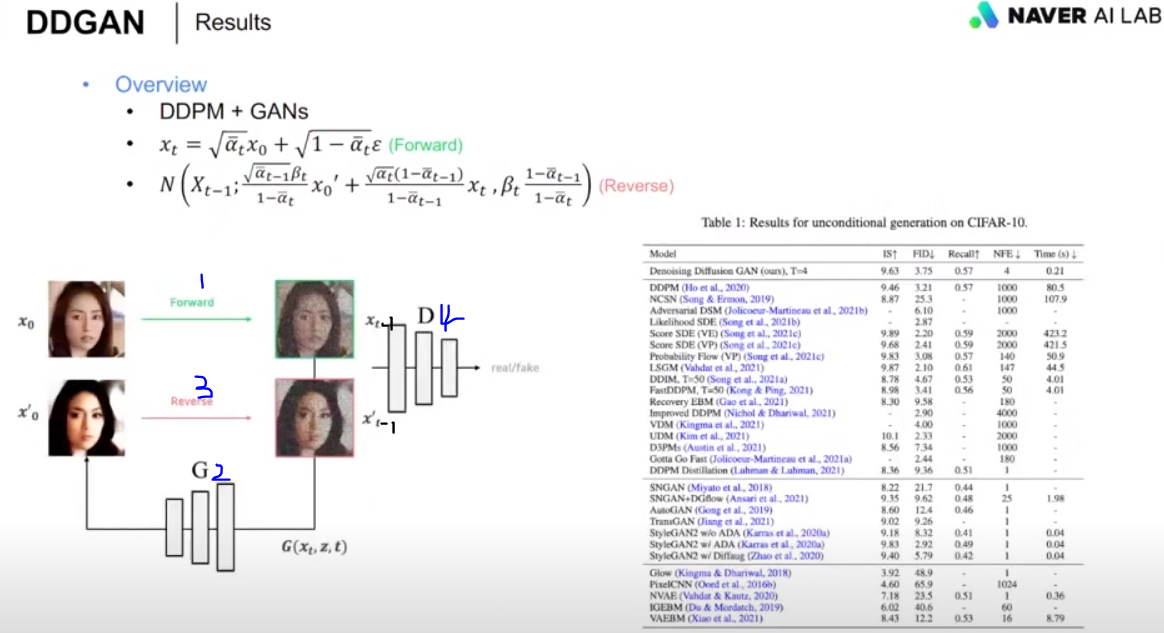
GAN은 학습하는 과정이 사실 diffusion보다 불안정함. 단지 real/fake인가를 구분하는 loss 하나로 무엇인가를 생성하기 때문에 진짜에 가깝게 fidelity도 나오고, speed도 빠르지만, 그 계산과정에서 분포에 대한 학습이 불안정했기 때문에 다양성의 diversity는 떨어질 수 밖에 없음.
하지만 Diffusion은 모든 과정에서 노이즈를 추가하고 앱실론을 계산하면서 분포에 대한 학습을 탄탄히 하였기 때문에 diversity가 높고 fidelity도 좋은 반면, 기초학습을 탄탄히 하는 문제로 speed는 떨어짐.
마지막 TEST 및 요약

1. x에다 noise 더하는 과정 (forward)
2. 그걸 일반식으로 표현한 것이군. 앱실론 = 노이즈 (xt = forward 일반식)
3. xt에서 noise를 빼서 xt-1로 만드는 과정 (reverse). 분산은 상수z이니 신경쓸필요 없고 평균만 구하면 되겠군
4. 평균 뮤의 수식표현
5. 더한 noise, 즉 앱실론만 예측하면 되겠군
6. revserse 과정의 일반식 (xt-1 = reverse 일반식)
7. classifier의 guidance 군




댓글