Set : 집합
- 합집합, 교집합, 차집합등의 연산을 가능케 하는 집합으로 {값1,값2,값3} 이런식ㅇ로 이루어져 있음. 출력을 할 때에는 randomly하게 출력하기 때문에, index를 지정하여 출력이 불가하고, 집합안에 중복된 것은 알아서 하나만 출력.
- 딕셔너리와 형태 주의하여 쓰기
>>> c = {} # 이렇게 빈 중괄호를 치면, 빈 딕셔너리가 됨.
>>> type(c)
<class 'dict'>
>>> c = set() # 꼭 이렇게 set()이라고 지정해야 세트가됨.
>>> type(c)
<class 'set'>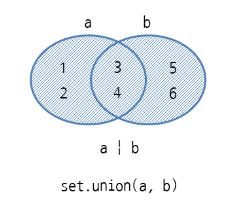
- set.union(세트1, 세트2) : 합집합 {1,2,3,4,5,6}
- 논리연산자 and와 같은 원리
- set.intersection(세트1,세트2) : 교집합 {3,4}
- set.difference(세트1, 세트2) : 대칭차집합 {1,2,5,6}
- 논리연산자 XOR ^와 같음
- set.symmetric_difference(대칭차집합)의 함수와 같음
- 현재세트.isdisjoint(다른세트) : 현재세트와 다른세트가 겹치는 요소가 없는가. (T: 없음 / F: 있음)
- 기호들
- |= : a + b = a.update(b)
- &= : 합집합의 요소만 현재 set에 새로 저장 = set1.intersection_update(set2)
- -= : set1에서 set2뺀 나머지만 출력 = set1.difference_update(set2) 와 같음
- ^= : set1과 set2에서 겹치는것만 빼고 다 합쳐서 출력 = set1.symmetric_difference(set2)
- <= : 부등호는 부분집합 여부를 뜻함. 인지 아닌지 T/F로 알려줌. = set1.issubset(set2)
- = 이 붙으면 self가 부분집합이 될 수 있는가 생각해야함. self는 self를 부분집합으로 가짐.
>>> a = {1, 2, 3, 4}
>>> b = {3, 4, 5, 6}
>>> a | b
{1, 2, 3, 4, 5, 6}
>>> set.union(a, b)
{1, 2, 3, 4, 5, 6}
>>> a & b
{3, 4}
>>> set.intersection(a, b)
{3, 4}
>>> a - b
{1, 2}
>>> set.difference(a, b)
{1, 2}
>>> a ^ b
{1, 2, 5, 6}
>>> set.symmetric_difference(a, b)
{1, 2, 5, 6}
>>> a = {1, 2, 3, 4}
>>> a.isdisjoint({5, 6, 7, 8}) # 겹치는 요소가 없음
True
>>> a.isdisjoint({3, 4, 5, 6}) # a와 3, 4가 겹침
False
--------------------------------------------------
>>> a = {1, 2, 3, 4}
>>> a |= {5}
>>> a
{1, 2, 3, 4, 5}
>>> a = {1, 2, 3, 4}
>>> a.update({5})
>>> a
{1, 2, 3, 4, 5}
>>> a &= {0, 1, 2, 3, 4}
>>> a
{1, 2, 3, 4}
>>> a = {1, 2, 3, 4}
>>> a.intersection_update({0, 1, 2, 3, 4})
>>> a
{1, 2, 3, 4}
>>> a -= {3}
>>> a
{1, 2, 4}
>>> a = {1, 2, 3, 4}
>>> a.difference_update({3})
>>> a
{1, 2, 4}
>>> a ^= {3, 4, 5, 6}
>>> a
{1, 2, 5, 6}
>>> a = {1, 2, 3, 4}
>>> a.symmetric_difference_update({3, 4, 5, 6})
>>> a
{1, 2, 5, 6}
-------------------------
>>> a = {1, 2, 3, 4}
>>> a <= {1, 2, 3, 4}
True
>>> a.issubset({1, 2, 3, 4, 5})
True
>>> a = {1, 2, 3, 4}
>>> a < {1, 2, 3, 4, 5}
True
>>> a = {1, 2, 3, 4}
>>> a >= {1, 2, 3, 4}
True
>>> a.issuperset({1, 2, 3, 4})
True
>>> a = {1, 2, 3, 4}
>>> a > {1, 2, 3}
True. add (요소) : 추가
.remove(요소) : 지울 값이 없으면 에러발생.
.disregard(요소) : 지울 값이 없으면 넘어감.
.pop(요소) : 지우고 지운 값을 출력함. 없으면 에러발생
.clear(요소): 모든요소 삭제
.len(세트) : 요소 갯수(길이) 구함
.copy() : 셋트 복사
for문으로 요소 다 꺼내올 수 있음
세트 복합식 가능 (comprehension)
>>> a = {i for i in 'apple'}
>>> a
{'l', 'p', 'e', 'a'}
>>> a = {i for i in 'pineapple' if i not in 'apl'}
>>> a
{'e', 'i', 'n'}
728x90
'Study (Data Science) > Python' 카테고리의 다른 글
| 프로그래머스) 배열의 평균값, 중복된 숫자갯수, 피자나눠먹기 (0) | 2022.11.28 |
|---|---|
| 프로그래머스) 머쓱이네 양꼬치 (0) | 2022.11.28 |
| 조별학습) 평균구하기 (딕셔너리) (0) | 2022.11.28 |
| UNIT 25. 딕셔너리 응용 (0) | 2022.11.28 |
| 오답노트) 간단명료 코드 만들기 (0) | 2022.11.28 |




댓글