0️⃣ 왜 아직도 DNN을 배워야 하나?
✔️ 목적
- “Transformer 시대인데 DNN을 왜 배워?”
- → DNN은 모든 딥러닝의 문법
✔️ 핵심 메시지
- CNN, RNN, Transformer, LLM
👉 전부 DNN 위에 쌓인 구조 - Backprop, 활성함수, 표현학습 없으면 전부 성립 ❌
- CNN = DNN + 공간 구조
- RNN = DNN + 시간
- Transformer = DNN + Attention
- LLM = 초거대 DNN
1️⃣ DNN 이전과 이후 – 패러다임 전환

✔️ DNN 이전
Raw Data
→ Feature Engineering (사람)
→ Classifier (SVM, LR)
- 포인트 : 사람이 '무엇이 중요한지'를 정의하던 시대. 피쳐 엔지니어링과 분류기 학습이 완전히 다른 단계로 존재하고 있음.
- 사람이 Feature Engineering을 수행하다보니 데이터의 의미를 사람이 가설로 정의하게 됨
- 도메인이 바뀌면 피쳐를 처음부터 다시 설계해야 함
- 피쳐가 고정되어 있으므로 데이터가 늘어나도 Classifier는 더 똑똑해질 수 없음. 즉, 사람이 뽑아낸 피쳐가 성능의 90%를 결정
- 결국 지능은 사람이 설계하고, 컴퓨터는 계산만 함
✔️ DNN 이후
Raw Data
→ DNN (Feature + Decision 동시 학습)
- 포인트: 모델이 '무엇이 중요한지'를 학습하던 시대. 피쳐 엔지니어링과 분류기 학습 단계가 하나로 합쳐짐. DNN 이전에는 Feature가 '입력값'이었으나, DNN 이후에는 Feature가 '학습 대상'이 되며, 첫번째 layer에서 Feature engineering을 수행하게 됨.
- Feature Learning을 통해 어떤 특징이 중요한지조차 모델이 스스로 학습하여 결정
- Classifier와 단계가 통합되어 있기 때문에 loss로 backpropagation 할 때 피쳐도 함께 영향을 받음. 즉, 피쳐가 중복되거나 분류에 방해가 된다면 그 피쳐를 버릴 수 있는 구조가 됨
- Feature selection이 학습과정에 내장된 구조 덕분에 End-to-End 학습이 가능해짐
- Case 1: 쓸모없는 feature
- 어떤 feacter z가 loss에 거의 기여하지 않으면, gradient도 거의 0이어서 해당 뉴런 가중치를 업데이트 하지 않게되어 사실상 그 피쳐는 무시되게 됨.
- Case 2: 해로운 feature
- 특정 feature가 오히려 오차를 키우면 gradient가 반대 방향으로 작용하며, 가중치가 감소하고, featuer가 소멸하게 됨
- Case 1: 쓸모없는 feature
- 레이어간 계층구조도 사람이 설계하지 않고, gradient descent 결과로 자연 발생
- 비선형 활성함수, 깊은 구조, Backpropagation으로 이가 가능하게 됨
- Scaling Law가 성립할 수 있게 됨
- Scailing law : 모델 크기(Parameters), 데이터양(Tokens), 연산량(Compute)을 키우면 loss 가 거의 직선처럼 예측 가능하게 감소한다. 즉, Scaling law는 AI연구를 예측 가능한, 측정 가능한 공학으로 바꿨다.
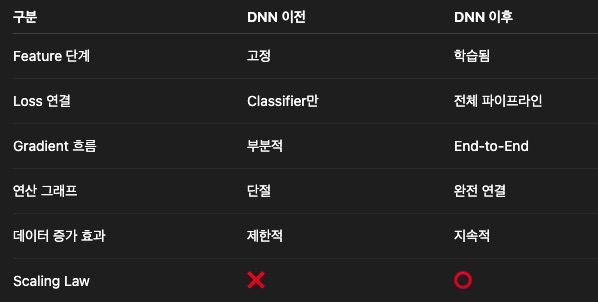
📌 왜 '새 알고리즘'보다 '모델을 키우는 것'이 더 확실할까
-> 알고리즘은 데이터 분포에 강하게 의존하기 때문에 특정 태스크에서만 효과가 좋다. 재현성이 낮아 효과 크기를 예측하기가 어렵고, 알고리즘 논문 100개중 실제로 표준으로 자리잡는 알고리즘은 극히 일부이기 때문에 알고리즘 개선은 불확실한 도약이다. 이에 비해 스케일링은 loss의 로그 스케일링에서 직선이라 계속된 감소를 보이는 loss가 확률적으로 보장된 하강곡선을 그린다. 그래서 새 알고리즘을 위한 아이디어를 기다릴 필요 없이 지금 당장 돈을 쓰면 성능이 오르기 때문에 OpenAI, Google, Meta는 새로운 알고리즘 아이디어를 기다리기 보다 연산자원 GPU에 더 투자하는 것이 확실한 성능 개선 전략이라고 판단하고 있다.
2️⃣ 퍼셉트론에서 DNN까지
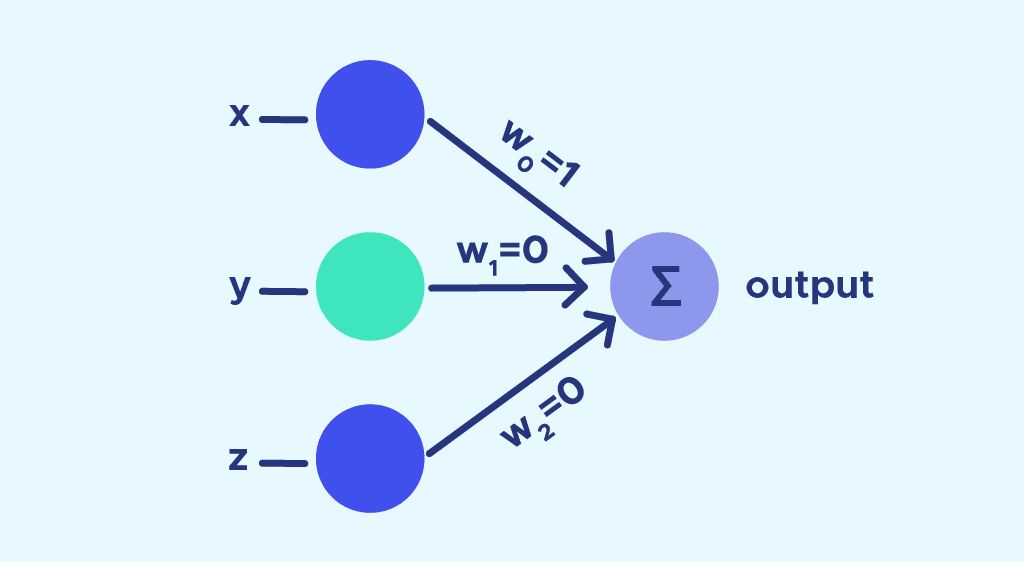

✔️ 단일 퍼셉트론 (Single Perceptron)
- z=w1x1+w2x2+⋯+b
- 여러 입력을 가중치로 섞어서 하나의 값으로 만든 '가중합'
- 선형 분류기
- XOR 문제 해결 불가



- XOR: 입력 둘이 서로 다를 때만 1(True), 둘 다 같으면 0(False)
- 그럼 어떤 직선을 그어도 안 되는 건가? ->안된다. XOR 데이터는 선형 분리(linearly separable)가 아니다.
- 만약 1번과 4번을 같은 쪽에 두려고 선을 그으면
→ 2번이나 3번 중 하나는 반드시 같이 묶임 - 2번과 3번을 묶으려 해도
→ 1번이나 4번이 끼어듦
- 만약 1번과 4번을 같은 쪽에 두려고 선을 그으면
- 단층 퍼셉트론 = 직선 하나, XOR = 직선 하나로 분리 불가하여, 퍼셉트론은 이 한계를 넘지 못했고, 인공신경망은 한계가 있다며 AI 겨울이 왔다.
- 이를 해결하기 위한 아이디어가 MLP 이다.
✔️ 다층 퍼셉트론: MLP (Multi-Layer Perceptron)

- 단일 퍼셉트론 여러층이 합쳐진 '가중합의 조합' 혹은 '표현의 조합'
- 1층 퍼셉트론이 만든 출력을, 2층 퍼셉트론이 다시 섞고, 3층이 또 섞음 -> 표현력 폭발
- 은닉층 + 비선형 활성함수
- 은닉층이 1개 이상
- XOR 해결
- 직선을 하나 더 만든다
- 은닉층 1개
- 직선 2개
- 공간을 접어서 재배치
- 직선을 하나 더 만든다
- 사용하던 활성함수: Sigmoid, Tanh
- MLP 자체로 개념에는 문제가 없었으나, 층이 깊어지면 깊어질 수록 뒤쪽 레이어만 학습되고, 앞쪽 레이어는 기울기 소실로 왜 틀렸는지를 회고하는 가중치 학습이 불가해졌다. 이유는 사용하던 활성함수에 있었다. sigmoid와 tanh의 그래프는 양끝에서 포화되도록 생겨 있어서 기울기(미분)의 최대치가 구조적으로 max 1이 넘지 못하게 제한되어 있었다. 하지만 Backpropagation은 곱셈구조다. 즉, 레이어 하나를 지날 때마다 미분값을 한 번 더 곺하게 되어있다. 1보다 작은 수의 반복곱셈은 언젠가 0으로 수렴한다. 예시로 미분값이 sigmoid max 값인 0.25라고 가정하고, 5층을 쌓아보면, 1층: 0.25 -> 2층: 0.0625 ->... 5층: 0.00098로 5층만 가도 거의 0이 되어버린다. 그래서 층이 깊어질수록 gradient가 곱해지면서 기울기가 소실되었고 (Gradient Vanishing), 3-5층을 넘어가면 학습이 붕괴되어 버렸다. 그리고 학습을 늘릴 데이터도 없었다.
- 그러던 중 ReLU 활성함수가 나오면서 깊은층을 쌓아도 학습이 가능하게 되고, DNN이 시작된다.

✔️ DNN
- 은닉층을 깊게 쌓음 (보통 3개 이상) = 깊은 MLP
- 깊은 표현(계층적 표현)이 가능
- ReLU: 양끝이 수렴하지 않아 sigmoid나 tanh처럼 기울기가 눌리는 구조적 문제가 없다. 그래서 아주 단순히 입력값 x가 양수면 x값 그대로 출력하고, 음수면 그냥 0으로 출력하여 차단한다. 미분값도 1 아니면 0이다. 또한 활성구간에서는 미분이 1이라 기울기가 보존되고, 비활성구간에서는 미분이 0이라 학습 신호가 차단된다. 이 단순한 스위치 구조 덕분에 깊은 신경망에서도 기울기 소멸 문제가 크게 완화되어 forward, backward 모두 안정적인 학습이 가능해져서 실질적 딥러닝 학습이 시작되었다.

3️⃣ DNN의 핵심 3요소
1. 퍼셉트론


- 입력 × 가중치 + bias
- 활성함수 적용
- 층을 거치며 변환
2. 활성함수
✔️ 왜 필요한가?
- 선형변환은 이런 형태다. y=Wx+by
- 선형 + 선형 + ... 아무리 선형변환을 여러번 겹쳐도 결국은 하나의 선형 변환으로 접힌다.
y=W2(W1x+b1)+b2 -> y=(W2W1)x+(W2b1+b2) - 층을 1개 쓰든, 10개 쓰든, 100개 쓰든 선형이고, XOR같은 비선형 문제는 절대 못푸는, 표현력이 떨어지는 구조이다.
- 하지만 비선형은 다르다. 비선형이 들어오는 순간 공간을 변형하고, 개념을 조합하고, 패턴을 분리할 수 있다. XOR도 풀이 가능하다.
- 그래서 비선형 활성함수가 DNN의 핵심요소가 된다.
- 표현력: 입력과 출력 관계를 얼마나 복잡한 함수로 표현할 수 있는가.

✔️ 대표 함수
- Sigmoid / Tanh → Gradient Vanishing
- ReLU → 현대 DNN 표준
3. Backpropagation

✔️ “출력 에러가 왜 첫 번째 층 가중치까지 영향을 줄 수 있을까?”
✔️ 핵심 아이디어
- Chain Rule
- 오차를 뒤로 전달
- 모든 가중치를 미분으로 업데이트
✔️ 수식은 최소화
- “미분의 연결” 개념만 강조
- 그림 + 흐름 위주
📌 “Backprop은 딥러닝을 가능하게 만든 유일한 이유다”
4️⃣ DNN이 가진 한계와 해결책

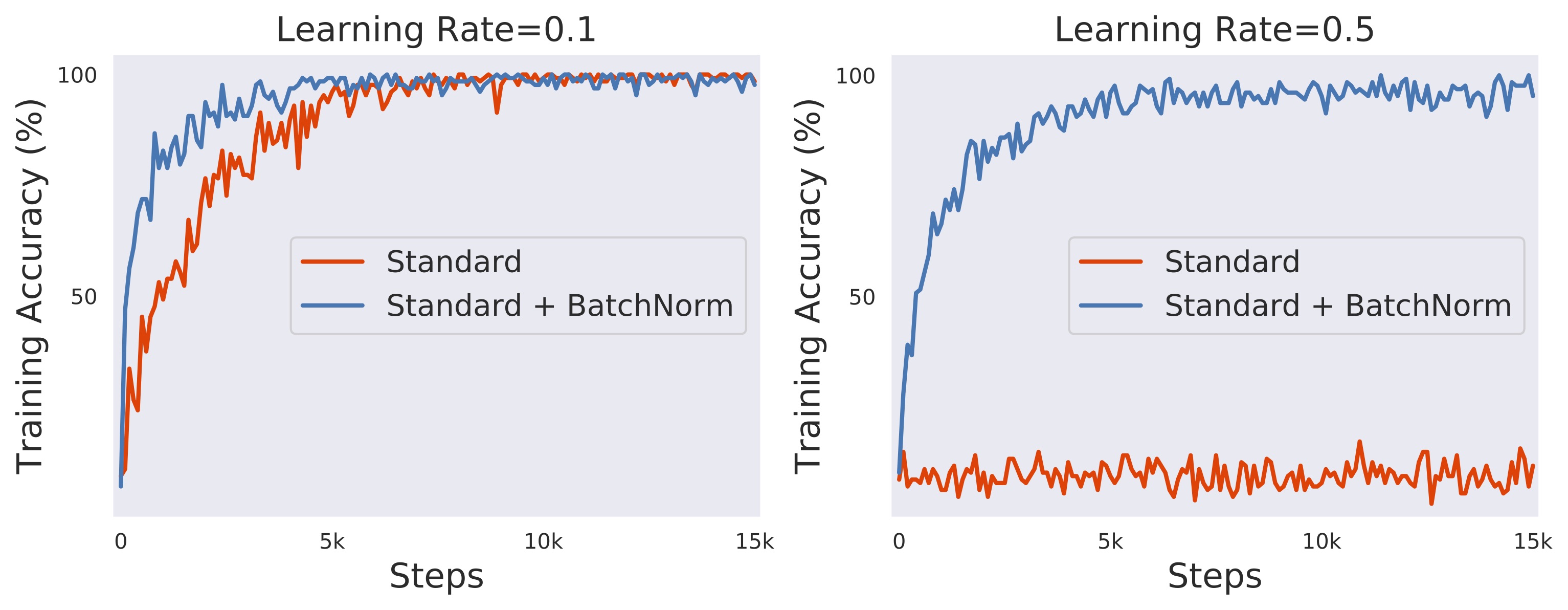
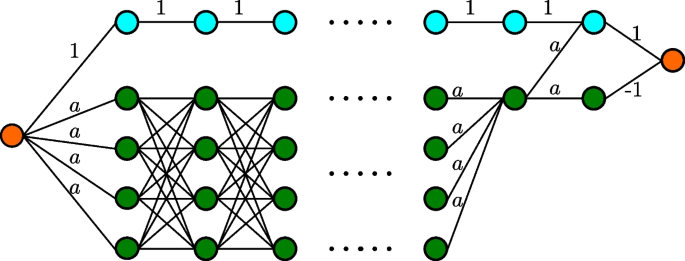
❌ 문제
- Vanishing / Exploding Gradient
- 학습 불안정
- 깊어질수록 학습 어려움
✔️ 해결
- ReLU
- Initialization (Xavier, He)
- Batch Normalization
- Residual Connection (다음 강의 떡밥)
📌 메시지“DNN은 이론보다 공학이 먼저 발전했다”
5️⃣ DNN → 현대 AI로의 연결
✔️ 연결 고리
- CNN = DNN + 공간 구조
- RNN = DNN + 시간
- Transformer = DNN + Attention
- LLM = 초거대 DNN
📌 마무리 한 문장“DNN은 모델이 아니라,
현대 AI의 사고방식이다”
728x90
'Study (Data Science) > NLP' 카테고리의 다른 글
| Langchain / Retriever (0) | 2024.05.23 |
|---|---|
| Langchain / Splitter (1) | 2024.05.23 |
| Langchain / Document_loader (0) | 2024.05.23 |
| 데이터를 많이 줄래, 에포크를 많이 줄래? (0) | 2024.05.21 |
| PDF file - RAG (0) | 2024.05.21 |



댓글