확률과 통계

1. 확률 (Probability)

from aiffel lms

• 이항(discrete) / 연속(continuous)
• 서로 배타적(mutually exclusive) : 시행의 모든 시도에서 한 사건 발생 시 다른 하나사건이 발생하지 않을 경우
• 집합(set), 원소(elements), 사건(events), 부분집합(subset), 전체집합(universal set), 공집합(null,empty set)
• 교집합(intersection), 합집합(union), 같음(equality)
• 여집합(complementary set; Set - A), 차집합(difference; A-B != B-A in Union), 서로소집합(disjoint set; A and B are mutually exclusive)
• A1​,A2​,…,An​ 이 서로 배타적인 사건일 때,
  • P(A)=P(A1​)+P(A2​)+⋯+P(An​)
  • P(A)=P(A∩B)+P(A∩Bˉ)
  • P(A∪B)=P(A)+P(B)−P(A∩B)
  • P(A∪B∪C)=​P(A)+P(B)+P(C)−P(A∩B)−P(A∩C)−P(B∩C)+P(A∩B∩C)​

---

2. 조건부 확률 (Conditional Probability)

• P(B∣A) : 확률이 00이 아닌 두 사건 A와 B에 대하여 사건 A가 일어났을 때, 사건 B가 일어날 확률
• 확률의 곱셈정리

[확률의 곱셈정리] 각각의 분모를 곱해 없앰

• 전확률 (Total probability)

from aiffel lms

• 베이즈 정리(Bayes' theorem) : P(B)의 확률을 알고 있을 경우,

독립(independent)

• 두 사건 A, B에 대해서 한 사건이 다른 하나의 사건에 영향을 주지 않을 때  A 와 B는 독립(independent)이다
  • P(A∣B)=P(A), P(A∩B)=P(A)P(B)
• 종속(dependent) : 독립의 반대 의미
• 독립인가, 종속인가?
  • 동전 앞면과 뒷면이 나오는 사건의 경우, 이 둘은 상호 배타적이며, 종속적이다. (독립X)
  • H를 앞면이 나올 경우, T를 뒷면이 나올 경우,
  • A={H}, B={T},  A∩B={∅} -> P(A∩B)=P(∅) -> P(A∩B)=P(∅)=0  :  상호 배타적 사건
  • P(A)=1/2, P(B)=1/2 , P(A∣B)=0 -> P(A∣B) != P(A), P(A∩B)=0 != 1/4=P(A)P(B) : 독립이 아님, 종속임. 

---

3. 확률 변수(random variables) 

• X(w) or X : 표본공간이 오메가, 표본공간의 한 표본점이 w일 때, w를 실수 상의 하나의 값으로 매빙(대응) 시켜주는 함수  = w를 하나의 실수로 바꿔주는 역할을 하는 함수
• x : 이 때, w라는 표본점이 확률 변수 X에 의해 매핑된 하나의 실수.
• Ax : A는 사건. 즉 w가 x로 매핑된 사건.
  • 사건이므로 확률을 가지고 있음. Ax​={w∣X(w)=x}={X=x}  >> p=P(Ax​)=P(X=x)
• 2개의 동전을 차례로 던질 경우,
  • 나올 수 있는 모든 수 : (앞,앞),(앞,뒤),(뒤,앞),(뒤,뒤)
  • 1,2,3,4에 매핑 : X((앞,앞))=1,X((앞,뒤))=2,X((뒤,앞)=3,X((뒤,뒤))=4
  • 여기서 X가 각 경우의 수를 하나의 실수로 매핑시키는 확률변수가 됨.
    • X의 값이 3일 확률은 P{X=3}=1/4
    • X의 값이 3 이하일 확률은 P{X≤3}=3/4
    • X의 값이 3 초과일 확률은 P{X>3}=1/4
    • X의 값이 1과 4 사이일 확률은 P{1<X<4}=1/2

분포 함수(distribution function) or 

누적 분포 함수(cumulative distribution function, CDF)

 

• FX​(x): 확률 변수X가 x보다 같거나 작을 확률

 

CDF 공식 (확률 변수 X 가&nbsp; x 보다 같거나 작을 확률)

 

• FX(x)는 단조 증가함수(monotonic increasing function) ; y = x나 y = log x처럼 감소하지않고 꾸준히 증가하는 함수.

이산 확률 변수(discrete random variables) 

확률 변수 X의 값인 x가 셀 수 있는 함수 (countable) 집합일 때.

자연수 집합은 countable, 실수(e.g. 0-1사이의 소수들) 집합은 uncountable 함.

• 확률 질량 함수(probability mass function, PMF) :  FX​(x) = 이항 확률변수
  • 확률질량함수의 누적분포함수는 계단함수(step function)의 형태를 보임

x의 확률질량함수 = 확률변수 X가 k일때의 확률의 합

from aiffel lms

연속 확률 변수(continuous random variables) 

확률 변수 X가 셀 수 없는(uncountable) 집합에서 정의될 때. (e.g. x가 0.00.0~1.01.0인 경우)

 

확률 밀도 함수(probability density function, PDF) : PMF 와 달리 셀 수 없으므로 밀도가 됨

from aiffel lms

기댓값 (expectation or expected value or mean)

• E[X] : 확률 변수 X가 있을 때, X의 기댓값
• 이산 확률 변수 X의 기대값은 각 X의 값에 그 값에 해당하는 확률을 곱하여 모두 더한 값이라서, X의 값에 곱하는 확률을 흔히 X의 값에 대한 '가중치'를 곱한다고도 표현함.
• 어떤 상수 c에 대해서 E[c]=c
• 기댓값은 확률 변수 X ,Y와 상수 a, b가 주어졌을 때, E[aX+bY]=aE[X]+bE[Y]

분산 (Variance)  = 표준편차(standard deviation)의 제곱

표준편차 = 분산에 루트씌운것

• 표준편차 (시그마)
  • 기댓값 - 평균 or 기댓값 - 중앙값 = E[(X−m)]
  • 표준편차가 작다 = 기댓값이 평균에 가깝다.
• 분산 (시그마의 제곱)
  • 확률 밀도 함수나 확률 질량 함수가 얼마나 퍼져있는지 그 정도를 나타냄
  • 분산이 높을 수록 넓게 퍼져있고, 낮을 수록 어느 한 곳에 집중되어 있음.

finally, 분산 = E[X2] - (E[x]2)

from aiffel lms

조건부 기댓값(conditional expectation)

조건에 부합하는 경우의 기댓값

 '시험을 통과한' 학생들의 '평균' 시험 성적 의 경우, 조건 : 시험통과 / 기댓값 : 평균

P(A) = A사건이 일어날 확률

• 예시 : 각 면이 나올 확률이 모두 동일한 6면체 주사위를 던진다고 할 때, 짝수가 나온 경우의 결과값들의 평균은 얼마?
• 답 : 4
  • X : 주사위의 각 눈이 나올 경우를 그 눈의 수로 할당하는 확률 변수
  • A :  주사위를 던졌을 때 짝수가 나올 경우 P(A) = 2,4,6이 나오는 경우 = 3/6 = 1/2

P(A) =&nbsp;1/2

---

4. 분포 (distribution)

• 베르누이 분포 (Bernoulli distribution) : 결과가 성공 혹은 실패 두가지로만 나오는 실험, 동전앞뒤실험 (베르누이 실험)의 확률변수 X (Bernoulli random variable)를 확률질량함수(PMF)로 표현한 것.

성공과 실패할 확률

성공은 1, 실패를 0으로 하는 확률변수X에 매핑

위와 같은 식. x가 0,1경우.

P(1) = p (p1승 x p0승(p의 0승은 1))

P(0) = 1-p   (1 x (1-p))

베르누이 확률변수 X의 누적분포함수 (CDF)

기댓값은 요소 x와 P(x)의 합이니,

E[X] = 0 x P(0)   +  1 x P(1)

베르누이 확률변수 X의 기댓값 = 성공확률(p)

E[X] = 0 x P(0)   +  1 x P(1)

베르누이 확률변수 X의 분산

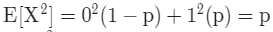
이항 확률 변수(binomial random variable) (Countable)

 

• 이항확률변수의 확률질량함수(PMF) = 이항분포
• 이산확률변수의 분포가 이항확률변수이고,
• 이항확률변수의 확률질량함수가 이항분포이다.
• 독립적으로 n번의 베르누이 시도를 했고, 그 중 성공한 수를 X(n)로 표현할 때, 이 X(n)이 이항확률변수
• X(n) = (n,p)   / n : 시행횟수, p = 성공할확률
  • 파라미터 n과 p에 의한 이항 분포를 띄는 이항 확률 변수 X(n)이라는 뜻
• 이항분포 (binomial distribution) = 이산확률질량함수 (PMF)  

이항분포 수식

1. 이항 계수 (binomial coefficient)
   • 가장 앞에있는 (n x) : x번의 성공과 n−x번의 실패를 할 경우의 수
   • 수식으로 표현하면, n​Ck​ = n! / x!(n−x)!

• 이항분포의 모양은 파라미터 n과 p에 의해 결정된다.
• 만약 p = 0.5이면, 이항 분포의 그래프는 평균값을 기준으로 좌우 대칭이 된다.

• 이항분포의 기댓값

• 이항분포의 분산
  • 하기공식에 따라,

위 식에서 m=x−2라고 둔다면, x=2일때 m=0이 되며 x=n일 땐 m=n−2

라고 작은 결론이 남.

위의 공식 좌변만 정리

분산 구하려고 E[X2n)]에 대해 정리

 

다시 위의 분산공식에 따라 정리하면,

위에서 공부한 CDF 공식으로 이항 CDF 구하기.

이항 확률변수 X(n) 의 누적확률분포(CDF) 공식

• Q3.어떤 볼링 선수가 스트라이크를 할 확률이 80%라고 할 때, 이 선수가 3번을 던져 2번 이상 스트라이크를 할 확률을 구해보세요.
• 풀이 
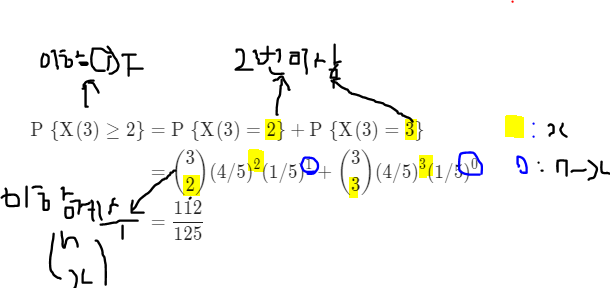
  • 2번 이상 성공할 누적확률을 구하는 것.  = 누적확률분포를 구하라는 것
  • n(횟수) = 3 /  p(성공확률) =0.8 = 4/5  /  x(몇번이상) = 2
  • 2번 이상 스크라이크 할 확률은

두번째줄 참고식

정규 확률변수 (normal random variable) (Uncountable)

정규확률변수

참고) 위의 이항확률변수

• 연속확률변수의 분포가 정규확률변수이고,
• 정규확률변수의 확률밀도함수가 정규분포이다.
• 정규분포 (normal distribution)
  • 정규 분포의 그래프는 μX​를 기준으로 대칭이며 종모양, 이항 분포 때와 비슷하게 μX​는 평균값이며, σX2​는 분산
  • 이항 분포의 n(횟수) =  μX //   p(성공할확률) = σX2.
  • 이항과 다르게 실수는 uncountable 하기 때문에 횟수를 셀수가 없어서 평균을 주고,  성공확률도 분산으로 대체.
  • 표준 정규 분포(standard normal distribution) : μX​=0, σX2​=1인 경우의 확률 분포 N(0,1)
  • 표준 정규 확률 변수(standard normal random variable)  : N(0,1)

• 정규분포의 누적분포함수(CDF)

CDF 공식 (확률 변수 X 가&nbsp; x 보다 같거나 작을 확률)

 

기댓값 공식

표준화를 위해 γ=(u−μX​)/σX​로 치환을 한다면, du=σX​dγ 가 됨으로 이를 위 식에 대입하면 다음과 같이 정리

 

누적분포함수

• 이항 분포의 n(횟수) =  μX(평균값) = 3 //   p(성공할확률) = σX2(분산,표준편차의제곱) = 9

문제 : Aiffel 3기의 학생 60명의 키는 평균이 170cm, 분산이 25cm인 정규분포를 따른다고 할 때, 표준 정규 분포표를 이용해 다음의 답을 구해보세요.

 

1. 키가 180cm 이상인 학생은 전체의 약 몇 %인가요?

• N(170, 25)
• P(X>=180) 은 1에서 180 이하인 부분을 빼면 됨.
• 1 - Fx(180) 이고, 하기 식에 따라 
• 1 - P((180-평균) / 표준편차) = 1 - P((180-170) / 5) = 1-P(2.0) = 약 1-0.9772 = 0.0228

누적분포함수

2. 키가 155cm 이상 175cm 이하인 학생은 약 몇명 인가요?

• N(170,25)
• P (155<= X <=175) = Fx(175) - Fx(155) = P((175-170)/5) - P((155-170)/5)
• P(1.0) - P(-3.0) = P(1.0) - {1 - P(3.0)} = P(1.0) + P(3.0) - 1 = 0.8413+0.9987-1 = 0.84
• 총 60명 * 확률 0.84 = 약 50명

---

이항 분포와 정규 분포의 관계

• X(n)∼B(n,p)에서 이항 분포의 식

• p 혹은 1−p가 0에 아주 가깝지 않으며 n의 값이 충분히 크다면 이항 분포의 그래프는 (평균,분산) =  (np, np(1−p)) 인 정규 분포의 곡선에 가까워짐
• X(n)가 이항 확률 변수일 때, Z가 표준 정규 분포를 따르는 확률 변수Z≈N(0,1))면

• X(n)로 표현된 확률 P(a≤X≤b),

•  n이 낮을 때는 모양이 조금씩 다르지만, n이 커지면 커질수록 모습이 같아짐
• 농구선수가 자유투를 10번 던졌을 때, 골을 넣은 횟수가 4개 이상 7개 이하일 확률을 구하세요. (골을 넣을 확률은 1/2 입니다.)

• 이항 분포를 이용해 근사한 표준 정규 분포를 이용해 구해보세요.(표준 정규 분포 표를 보고 구하세요.)
• N (np, np(1-p) = (10*0.5 , (10*0.5)0.5) = N(5, 2.5)
• P (4<= X <=7) = Fx(7) - Fx(4) = P((7-5)/2.5) - P((4-5)/2.5) = P(1.26) - {P(-0.63)} =  P(1.26) + P(0.63) - 1 = 0.6319

• 이항 분포를 이용한 확률

 

n이 커질수록 위의 두 확률은 비슷해지게 된다.