시계열 예측(Time-Series Prediction)을 다루는 여러 가지 통계적 기법
- ARIMA(Auto-regressive Integrated Moving Average)
- 페이스북 Prophet
- LSTM Layer
시계열 예측의 예시
- 지금까지의 주가 변화를 바탕으로 다음 주가 변동 예측
- 특정 지역의 기후데이터를 바탕으로 내일의 온도 변화 예측
- 공장 센터 데이터 변화 이력을 토대로 이상 발생 예측
예측을 위한 전제 2가지
- 과거의 데이터에 일정한 패턴이 발견된다.
- 과거의 패턴은 미래에도 동일하게 반복될 것이다.
>>>> 즉, 안정적(Stationary) 데이터에 대해서만 미래 예측이 가능하다.
- 안정적(Stationary) : 시계열 데이터의 통계적 특성이 변하지 않는다 / 시계열 데이터를 만들어내는 시간의 변화에 무관하게 일정한 프로세스가 존재한다
- 다른 데이터를 추가하여 활용한다면 엄밀한 의미의 시계열 데이터 예측은 아니다. 외부적 변수에 의해 안정성이 훼손될 수 있기 때문.
안정적(Stationary) : 시계열 데이터의 통계적 특성이 변하지 않는다
- 시간이 흘러도 일정해야 하는 통계적 특성들 (일정해야 하는 구간 통계치들)
- 평균 (이동평균)
- 분산 (이동표준편차)
- 공분산 (자기공분산)
수학적 개념이해
- 평균
평균은 말그대로 평균입니다. 모든 데이터를 더하고 그 개수(n)로 나눈 값이죠.

- 분산(Variance. VAR(X))
- 분산은 데이터들이 평균에서 얼마나 떨어져 있는지 가늠하기 위한 지표입니다.
- 편차의 제곱의 평균

- 공분산(Covariance. COV(X, Y))
공분산은 변수가 두 개 일때의 분산입니다. 각 변수의 분포가 서로 얼마나 관련이 있는지를 수치적으로 표현한 것으로 이해할 수 있으며, 각 변수의 평균에서의 편차를 곱한 것의 평균이라고 정의합니다. - 2개의 확률변수의 선형 관계를 나타내는 값. 만약 2개의 변수중 하나의 값이 상승하는 경향을 보일 때 다른 값도 상승하는 선형 상관성이 있다면 양수의 공분산을 가진다
- 두 변수의 편차끼리의 곱의 평균

- 상관관계(Correlation. COR(X,Y))
상관관계는 공분산을 각 분산으로 다시 나누어주어 공분산을 (-1,1) 범위로 스케일링 해준 것이라고 볼 수 있습니다. 두 변수가 양의 관계에 가까울수록 1, 음의 관계에 가까울수록 -1, 관계가 무관해보일수록 0에 가깝습니다. - 두 변수의 공분산 / 두 변수의 편차의 곱의 루트

- 이동평균(Moving Average. 혹은 Rolling Mean)
- 시계열 데이터에서 특정 개수(d)의 데이터를 시점(t)을 이동하며 계산하는 평균입니다.
- 전체 데이터 집합의 여러 하위 집합에 대한 일련의 평균을 만들어 데이터 요소를 분석
- 시간의 어느 시점을 t라고 지정하여 시간의 구간을 만들고 그 구간 갯수는 d, 구간평균들의 평균.

- 이동표준편차(Rolling std)
이동표준편차란 시계열 데이터에서 특정 개수(d)의 데이터를 시점(t)을 이동하며 계산하는 표준편차입니다. (표준편차는 분산에 제곱근을 씌운 값입니다.

- 자기공분산(Autocovariance)
- 자기공분산이란 일정 시차(h)를 둔 자기 자신과의 공분산입니다.
- 공분산은 X,Y (서로다른변수) 간의 관계였지만, 자기공분산은 X 변수 하나 안의 s 시점과 t 시점간의 공분산

- 자기상관계수(Autocorrelation)
- 자기상관계수란 일정 시차(h)를 둔 자기 자신과의 상관계수입니다.
- 상관계수는 X,Y (서로다른변수) 간의 관계였지만, 자기상관계수는 X 변수의 서로다른 시간차이 (time lag) 간의 관계

가장 중요한 것 : t에 무관하게 예측이 맞아떨어져야 한다는 점
직전 5년 치 판매량 X(t-4), X(t-3), X(t-2), X(t-1), X(t)를 가지고 X(t+1)이 얼마일지 예측한다 할 때,
t=2010일 때의 데이터를 가지고 X(2011)을 정확하게 예측하는 모델이라면
이 모델에 t=2020을 대입해도 이 모델이 X(2021)을 정확하게 예측할 수 있어야함.
그렇지 않으면 t에 따라 달라져서
"과거의 패턴이 미래에도 반복될 것"이라는 시계열 예측의 대전제를 무너뜨리게 되고,
그때그때 달라요 예측이 됨.
- 이동평균, 이동표준편차가 일정해야함
- (t에 무관하게 X(t-4), X(t-3), X(t-2), X(t-1), X(t)의 평균과 분산이 일정 범위 안에 있어야 함)
- 자기공분산이 일정해야함
- (= X(t-h)와 X(t)는 t에 무관하게 h에 대해서만 달라지는 일정한 상관도를 가져야함)
- 귀무가설(Null Hypothesis) : ~와 같다, 차이가 없다, 효과가 없다
- p-value(유의확률) : 귀무가설이 참이라고 가정했을 때, 표본으로 얻어지는 통계치(예: 표본 평균)가 나타날 확률
- p값이 낮다 : 귀무가설이 참이라는 가정 하에 표본추출시, 이런 표본 평균이 관측될 확률이 낮다.
- p값이 매우 낮으면 (0.05 미만), 이런 표본 통계량은 우연히 나타나기 어려운 특별한 케이스가 되어 귀무가설을 기각하고, 대립가설을 채택하게 됨.
- 대립가설(Alternative Hypothesis) : ~와 다르다, 차이가 있다, 효과는 있다
Augmented Dickey-Fuller Test(ADF Test)
- 정상성을 알아보기 위해 1979년 David Dickey와 Wayne Fuller에 의해 개발된 DF 검정을 일반화한 단위근 검정 방법.
- 단위근(unit root) : , y=1인 해로, 시계열 자료에서 예측할 수 없는 결과를 가져올 수 있음. 있으면 불안정.

- 귀무가설 (
- 검정통계량이 Critical Value보다 작거나, p-value가 설정한 유의수준 값보다 작으면 정상적인 시계열 데이터
- statsmodels 패키지의 adfuller 함수를 이용 (주어진 timeseries에 대한 ADF test를 수행하는 코드)
시계열 분해(Time series decomposition) (with. ADF Test)
시계열 분해 과정
1. 로그함수 변환 : 시간에 따라 분산이 점점 커질 때, 로그함수로 변환해주면 분산이 안정화될 수 있음.
2. Moving average 제거 - 추세(Trend) 상쇄하기
- 추세(trend) : 시간 추이에 따라 나타나는 평균값 변화 / 이동평균을 ts_log에서 빼주기
3. 차분(Differencing) - 계절성(Seasonality) 상쇄하기
- 차분 (Differencing) : 연이은 관측값들의 차이를 계산하는 것. 시계열의 평균 변화를 일정하게 만드는데 도움을줌.
- 계절성(Seasonality) : trend에는 잡히지 않지만, 패턴이 파악되지 않은 주기적인 변화 .
계절성은 예측에 방해되는 불안정한 요소.
이동평균을 뺀다고 상쇄되는 효과가 아님.
이번 스텝의 변화량 = 현재 스텝 값 - 직전 스텝 값 - 1차 차분 후에도 p-value가 떨어지지 않으면 2차 차분을 하기도 함.
- 2차 차분 : 변화에서 나타나는 변화. (현재 - 한스텝전) - (한스텝전 - 두스텝전)
실행방법




ARIMA 모델
AR(Autoregressive) + I(Integrated) + MA(Moving Average)
위의 시계열 분해를 통한 시계열 데이터 예측 모델을 자동으로 만들 수 있음
모델 설명
- AR (자기회귀, Autoregressive)
- 지금의 Y = 한스텝, 두스텝... p스텝전의 Y들의 합 (과거의 내모습 = lag (시차))
- Y는 이미 trend, seasonality 다 뺀 Residual임. 즉 residual을 모델링함.
- 지금의 나 = 과거의 나들의 합
- 지금의 주식값 = 이전의 주식값들의 합.. 결국 일정 값수준으로 균형을 유지할 것이라 예측하는 관점
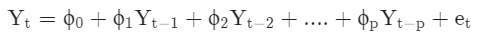
- MA (이동평균, Moving Avg)
- 지금의 Y = 한개, 두개... q개 전에 예측한 오차들의 합
- 오차 = 트렌드. 곧 trend 부분에 대한 모델링임.
- 지금의 주식값 = 증감패턴 (이말 자체가 trend) 을 지속할 것이라고 보는 관점

- I (차분누적, Integration (about differencing))
- 지금의 Y = 이전데이터와 d차 차분의 누적합 = 이전데이터 + 변화량
- 보통은 2차차분까지 가지 않고 1차차분으로 마침..

주식값이 떨어진 것을 알게되었을 때,
- '오늘은 주식이 올라서 균형을 맞추겠지?'라는 AR 형태의 기대와
- '어제 떨어졌으니 추세적으로 계속 떨어지지 않을까?'라는 MA 형태의 우려가 함께 나타남
ARIMA 는 AR, MA 두 모델 사이에서 적정 수준을 찾아감.
ARIMA의 parameter 세 가지
- p : AR의 시차, 찻수
- d : I 차분누적 횟수
- q : MA의 시차, 찻수
Parameter 정하는 방법
p 와 q 는 일반적으로 p + q < 2, p * q = 0 인 값을 사용하는데, 이는 p 나 q 중 하나는 0이라는 뜻.
이렇게 하는 이유는 많은 시계열 데이터가 AR이나 MA 중 하나의 경향만 가지기 때문.
ACF (Autocorrelation Function)
- 시차(lag)에 따른 관측치들 사이의 관련성을 측정하는 함수
- 주어진 시계열의 현재 값이 과거(y_{t-1}, y_{t-2}, ...., y_{t-n}) 값과 어떻게 상관되는지 설명함.
- ACF plot에서 X 축은 상관 계수를 나타냄, y축은 시차 수를 나타냄
- AR(p)에서는 점차적으로 감소하고, MA(q) 이후에 0이 되므로 q를 결정할 수 있음.
PACF (Partial Autocorrelation Fuction)
- 다른 관측치의 영향력을 배제하고 두 시차의 관측치 간 관련성을 측정하는 함수
- k 이외의 모든 시차를 갖는 관측치(y_{t-1}, y_{t-2}, ...., y_{t-k+1})의 영향력을 배제한 가운데 특정 두 관측치, y_{t}와 y_{t-k}가 얼마나 관련이 있는지 나타내는 척도.
- AR(p)에서는 0이 되고, MA(q) 에서는 감소하므로, p를 결정할 수 있음.

< ACF를 통해서 정상성을 알아보는 방법 정리 >
- 일정한 패턴이 없거나 갑자기 떨어지는 패턴 => stationary
- 일정하게 떨어지거나 올라갔다 내려갔다하면서 굉장히 천천히 떨어지는 패턴 => nonstationary
728x90
'Study (Data Science) > DL' 카테고리의 다른 글
| model.summary 에서의 param# 구하기 (0) | 2023.01.06 |
|---|---|
| 활성화함수 종류 (0) | 2022.12.29 |
| 인공지능, 머신러닝 그리고 딥러닝 (4) | 2022.12.27 |
| TF-IDF (0) | 2022.12.19 |
| Loss / Metric (0) | 2022.12.15 |




댓글